球形高斯近似
之前提到,这篇文章 介绍了通过 球形高斯近似 来优化 pow 的计算,代码如下:
优化前:
1
2
3
4
5
// Generalized Power Function
float pow(float x, float n)
{
return exp(log(x) * n);
}
优化后:
1
2
3
4
5
6
// Spherical Gaussian Power Function
float pow(float x, float n)
{
n = n * 1.4427f + 1.4427f; // 1.4427f --> 1/ln(2)
return exp2(x * n - n);
}
推导
关于上面代码的推导,可以参考 这篇文章,这里再列一下主要推导过程:
pow 的 球形高斯近似:
1
pow(nh, K) = exp(-K*(1-nh))
其中 exp 可以用 exp2 这样表示:
1
exp(a) = exp2(a/ln(2))
带入后得到:
1
pow(nh, K) = exp2(-(K/ln(2))(1-nh))
这里的 1 / ln(2) 是一个常量,约等于 1.4427f,我们可以提前计算好,再带入上面的公式:
1
pow(nh, K) = exp2(-(K*1.4427f)(1-nh)) = exp2(nh*K*1.4427f-K*1.4427f)
把 K*1.4427 提出来后可以得到:
1
2
float A = K * 1.4427
pow(nh, K) = exp2(A * nh - A)
用代码表示如下:
1
2
3
4
5
6
// Spherical Gaussian Power Function
float pow(float x, float n)
{
n = n * 1.4427f;
return exp2(x * n - n);
}
这个结果和文章最开头的优化代码还是有区别的,主要原因是 pow(nh, K) = exp(-K*(1-nh)) 这个近似对于 比较小的K 来说近似结果相差较大,作者做了一些对比,如下图:
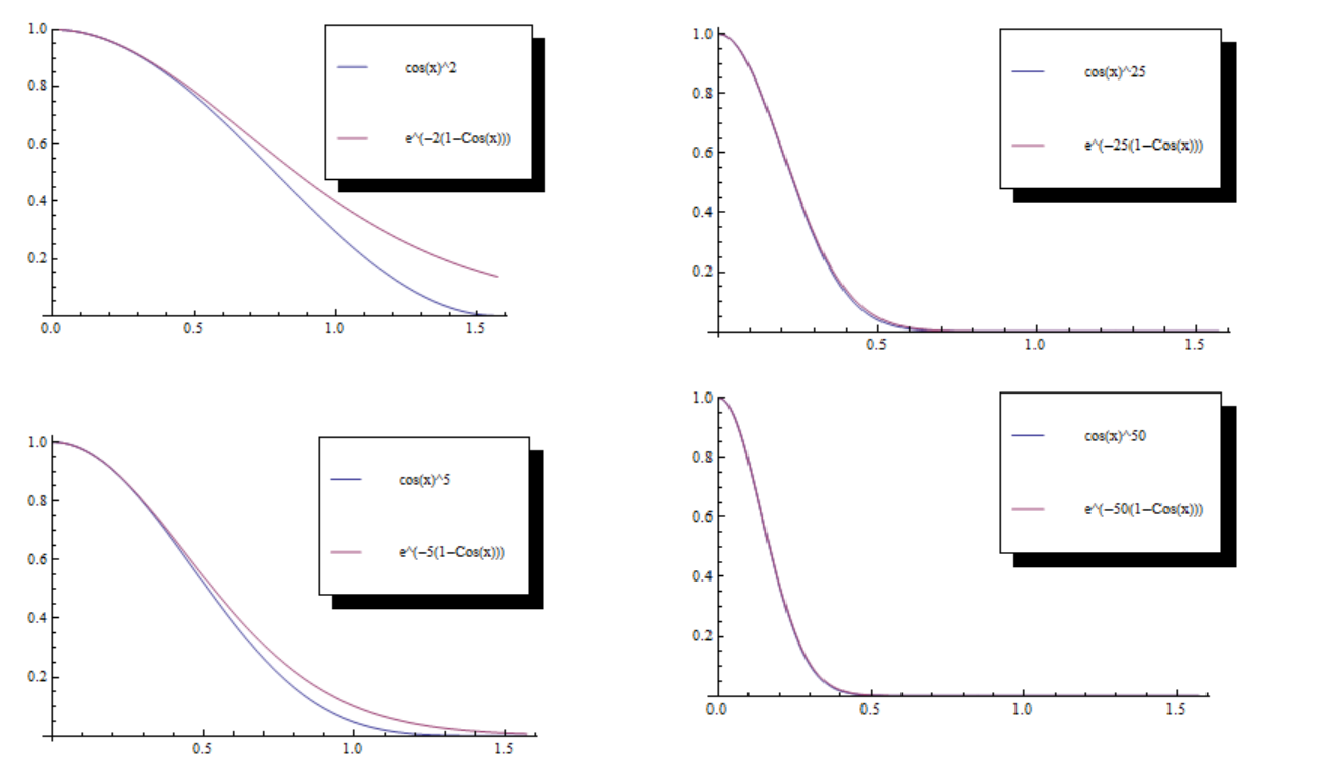
针对这个问题,作者也介绍了一个更好的近似方式,即给原先的公式添加一个常数,如下:
1
pow(nh, K) = exp((K+X)(nh-1))
可以看到,这里的 X 为 0 的时候就是之前的近似公式,作者建议 X 在 [0,1] 这个区间取值。
当 X 为 1 时,就是我们上面的优化代码:
1
2
3
4
5
6
// Spherical Gaussian Power Function
float pow(float x, float n)
{
n = n * 1.4427f + 1.4427f; // 1.4427f --> 1/ln(2)
return exp2(x * n - n);
}
下图是添加常数后 pow(cos(x), 2) 的近似效果对比,红色曲线是近似曲线,可以看到,近似效果还不错:
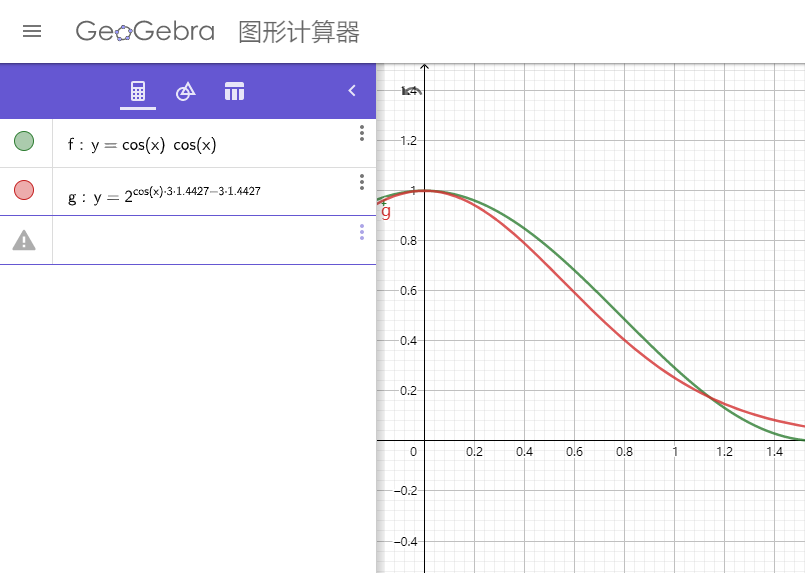
游戏里的效果
优化前:

优化后:

地表的高光几乎看不出什么差别。
其他
作者的总结:
This post provided an application of a SG approximation, where the goal was to save a few ALU instructions. Again, for modern GPUs, this is not necessarily beneficial, but for older mainstream hardware, such as the PS3 and XBOX360 GPUs, it is a quite useful tool to have in your pocket.
意思是对于现代 GPU,这样做可能意义不大,不过对于老一点的硬件,这个优化值得拥有。
好了,拜拜。